Metaman
Zainteresovan član
- Poruka
- 221
axaaaa... Hvala puno...
Donji video prikazuje kako da instalirate aplikaciju na početni ekran svog uređaja.
Napomena: This feature may not be available in some browsers.
Logaritmuj ceo izraz po osnovi e, dobićeš ln x = c * ln y + ln k. Onda na jednu osu naneseš ln x, a na drugu ln y, pa ćeš dobiti linearan grafik. Koeficijent pravca je c, a ln k će biti dužina odgovarajućeg odsečka na jednoj od osa.

evo da malo razbudim ove matematicare. Radi se o sledecem: imam funkciju x=ky^c, k i c su mi nepoznate konstante, a poznate su mi vrijednosti y za odredjeno x (koje je takodje poznato), tako da ja mogu nacrtati grafik koji naravno nije linearan... Meni treba da linearizujem ovu fukciju tako da mogu naci koeficijent pravca, preko koga cu naci neku od ovih nepoznatih konstanti (k ili c), e sad ja vas pitam kako da je linearizujem i da li je to uopste mguce?



@paganko ti si bas saljiv ponekad... Ja nisam ni ovo znao a kamo li to....Meni treba da nacrtam grafik koji je linearan i to sam ovako uradio, zatim odredio koeficijent pravca i gotovo... O tom razvijanju u red ja pojma nemam... :/
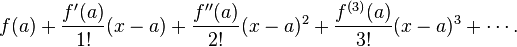
evo da malo razbudim ove matematicare. Radi se o sledecem: imam funkciju x=ky^c, k i c su mi nepoznate konstante, a poznate su mi vrijednosti y za odredjeno x (koje je takodje poznato), tako da ja mogu nacrtati grafik koji naravno nije linearan... Meni treba da linearizujem ovu fukciju tako da mogu naci koeficijent pravca, preko koga cu naci neku od ovih nepoznatih konstanti (k ili c), e sad ja vas pitam kako da je linearizujem i da li je to uopste mguce?





treba mi mala pomoc: kako mogu rijesiti jednacinu tipa x^x=a??

Jok Beogradska Poslovna Škola
