Је л' може неко да напише поступак како се из овога:
Pogledajte prilog 259198
добија ово:
Pogledajte prilog 259199
Хвала унапред
Pretpostavljam da je tu v' = 0 Onda samo središ izraz, ništa prostije...
Donji video prikazuje kako da instalirate aplikaciju na početni ekran svog uređaja.
Napomena: This feature may not be available in some browsers.
Је л' може неко да напише поступак како се из овога:
Pogledajte prilog 259198
добија ово:
Pogledajte prilog 259199
Хвала унапред

Osnovica AB trapeza ABCD je dva puta duza od osnovice CD i dva puta duza od kraka AD. Ako je dijagonala AC = 10 cm, a krak BD = 8 cm, odrediti povrsinu trapeza.
 Hvala unapred!
Hvala unapred! 
Molim vas, pomozite mi..ne znam da uradim zadatak.,Hvala unapred!

Како то мислиш да је КРАК BD=8? Да ниси погрешила неко слово или је можда у питању дијагонала?
 ja se izvinjavam.. pogresila sam..
ja se izvinjavam.. pogresila sam.. 
Не, не. Није нула. Нема везе шта је колико, него ми само треба поступак како се из "слике 1" стиже до "слике 2" поступно
Molim vas, pomozite mi..ne znam da uradim zadatak.,Hvala unapred!

 Je li to iz Krugove zbirke?
Je li to iz Krugove zbirke? I mene muci taj zadatak..Je li to iz Krugove zbirke?

Evo jos jednog:
Ako je d dijagonala strane kocke, izraziti u zavisnosti od d:
a) ivicu kocke
b) povrsinu kocke
v) zapreminu kocke


Hvala! Nisam znala za taj odnost, jos nismo ucili..
I mene muci taj zadatak..Je li to iz Krugove zbirke?

Evo jos jednog:
Ako je d dijagonala strane kocke, izraziti u zavisnosti od d:
a) ivicu kocke
b) povrsinu kocke
v) zapreminu kocke
 Jeste, iz Krugove zbirke je
Jeste, iz Krugove zbirke je 
Је л' може неко да објасни Метод најмањих квадрата? На неком обичном конкретном примеру. Не капирам уопште шта ја ту треба да радим :/



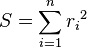











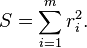

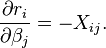










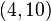
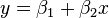

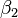


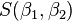

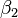
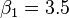



Pitanje u vezi limesa.
Kada zamenimo x koji npr. teži beskonačnosti u funkciju čiji limes u toj tački želimo da nađemo i otrkijemo da je u tom slučaju: beskonačno - beskonačno
i onda izraz npr. faktorizujemo i dobijemo konačan limes. Pitanje je sledeće: Šta bi sa onim prvim kada smo dobili beskonačno - beskonačno i tada nismo mogli da odredimo limes,
a sada možemo. Zašto sada možemo?

Ako zna neko da reši, treba mi za sutra
Neki polinom pri dijeljenju sa (x-1) daje ostatak -1, pri dijeljenju sa (x-2) daje ostatak 5 i pri dijelenju sa (x-3) daje ostatak 15.Naći ostatak dijeljenja tog polinoma sa X[SUP]3[/SUP]+ 6X[SUP]2[/SUP]+ 11X -6
Osnovica AB trapeza ABCD je dva puta duza od osnovice CD i dva puta duza od kraka AD. Ako je dijagonala AC = 10 cm, a krak BD = 8 cm, odrediti povrsinu trapeza.
Ovog je oblika, i nisam promašio ništaNisi precizirao da li je polinom recimo ovog oblika :
P(x) = ax[SUP]4[/SUP]+bx[SUP]3[/SUP]+cx[SUP]2[/SUP]+dx+e

Ovog je oblika, i nisam promašio ništa
