Trigonometrija

[Baby Yoda]

Nikako ne mogu da shvatim da li je moguće odrediti na osnovu odnosa stranica tačnu dužinu samih stranica ako su sve one nepoznate, a uglovi poznati.

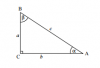
Kako izračunati sve stranice ako znamo da je ugao gama logično 90 stepeni, a dat mi je i ugao alfa koji je 45 stepeni. Ja sam koristio trigonometrijske formmule za odnose stranica i došao do podataka da je sinus i kosinus alfa koren iz dva sa dva. A da su tangens i kotanges ugla alfa (45 stepeni) , odnos 1. I onda se pitam kako ja mogu da izvučem iz tih odnosa koliko iznose stranice?

 

[ccaterpillar]

Не можеш да нађеш странице из простог разлога што имаш бесконачно много оваквих троуглова, рецимо можеш да их нацрташ један у другоме колико хоћеш.

Оно што можеш да урадиш јесте да друге две странице изразиш преко треће, рецимо ако ти је страница а позната, онда је страница b једнака а, а хипотенуза је овде а*sqrt(2)

 

[Baby Yoda]

Našao sam soluciju. Pošto postoji vektor koji ide na dole normalno na tačku A praveći ugao od 90 stepeni, napravio sam pravougaonik dodavši vektor i u tački C čime sam izračunao dijagonalu pravougaonika, a preko trigonometrije i stranicu b za trougao. Naravno vektor je imao poznatu vrednost.

 

[Ivan_10]

Pozdrav,
Nije mi jasno kako se ovde na kraju dobije da je alfa=0. Ako može neko da objasni postupno

 

[cronnin]

Pozdrav,
Nije mi jasno kako se ovde na kraju dobije da je alfa=0. Ako može neko da objasni postupno

Па јеси ли средио ово?
Зар се не добије на крају sin(2α)=2α тј. sinx=x?

 

[Bren]

Jeste. I kada nacrtaš y=x i y=sinx seku se samo u x=0. Ovu jednačinu je laako rešiti grafički.