Baraba na kvadrat
Elita
- Poruka
- 17.135
Moram da se pohvalim imao sam test iz fizike super sam prosao zadaci su bili kranje laki
-
- Popularno:
- In memoriam Dejan Ristanović
- Plesao 144 sata i oborio rekord u video...
- Sta sestra sestri moze da napravi
- Sta kada podstanari nece da napuste...
- Опадање критеријума с годинама ?
- Da li je moguce ...
- Poslednja vremena
- Pitanje za muškarce
- Studentska lista, sta se jos ceka?
- Crna Gora kreće na Rusiju!
- stanje
Moram da se pohvalim imao sam test iz fizike super sam prosao zadaci su bili kranje laki
dr, a koja si ti shkola kada radish ispitivanje funkcija u trecem razredu? xD
Baraba na kvadrat
Elita
- Poruka
- 17.135
dr, a koja si ti shkola kada radish ispitivanje funkcija u trecem razredu? xD
Ja sam gimnazijalac
Nismo mi to jos radili, osim za najobicniju kvadratnu i kubnu ali ja sam eto pametan
Ja sam gimnazijalac
Nismo mi to jos radili, osim za najobicniju kvadratnu i kubnu ali ja sam eto pametan
HAhahah, pa s obzirom da niste radili ni asimptote ni ponashanje na krajevima oblasti definisanosti, izvode, monotonost, stacionarne tacke, konveksnost, konkavnost, prevojne tacke itd. tesko da mozes da se bavis ispitivanjem xD
@Paganko: Hocemo dobiti reshenje
Imam sutra pismeni 
Baraba na kvadrat
Elita
- Poruka
- 17.135
HAhahah, pa s obzirom da niste radili ni asimptote ni ponashanje na krajevima oblasti definisanosti, izvode, monotonost, stacionarne tacke, konveksnost, konkavnost, prevojne tacke itd. tesko da mozes da se bavis ispitivanjem xD
@Paganko: Hocemo dobiti reshenje
Tacno tako
HAhahah, pa s obzirom da niste radili ni asimptote ni ponashanje na krajevima oblasti definisanosti, izvode, monotonost, stacionarne tacke, konveksnost, konkavnost, prevojne tacke itd. tesko da mozes da se bavis ispitivanjem xD
@Paganko: Hocemo dobiti reshenje
funkcija koju sam zadao definitivno nije za pismeni. za neki ispit, i to malo tezi, da ili nesto slicno.
takodje je i skolski primer da funkcija moze imati ekstremnu vrednost a da prvi izvod nije nula, zapravo da cak i ne postoji u toj tacki.
bila je to jedna od tezih funkcija koje sam imao prilike da ispitam kada sam vezbao za taj ispit, i mislio sam, pa ne moze teze od ovoga. bez pomoci digitrona treba jedno sat vremena peske racunati..... A onda mi je profesor pokazao da moze i teze. Zadao je neku ogavstinu koju sam radio ciglo 2 sata i to cistog tabananja jer sam bio uvezban da ne moze da me iznenadi. Secam se i da je uletela tu neka kvadratna logaritamska jednacina koja je bila u eksponentu pa sam blago je reci poludeo. Blagosloveni bili Matlab i Mathematica pa da ne moram to vise rucno raditi.
Evo i resenja koga zanima:
Pogledajte prilog 67783
Ma daj covece, ne zezaj me, ja se vec s*****o
))Dobio sam pet sa zvezdom, btw... JEDINI hahahah
Baraba na kvadrat
Elita
- Poruka
- 17.135
Ma daj covece, ne zezaj me, ja se vec s*****o
Dobio sam pet sa zvezdom, btw... JEDINI hahahah
Ma daj covece, ne zezaj me, ja se vec s*****o
Dobio sam pet sa zvezdom, btw... JEDINI hahahah
e svaka cast.
Imam standardni oblik kvadratnih (ne)jednacina: ax^2 bx + c.
Treba mi ne resenje vec uputstvo kako da tim sistemom resim ovakve zadatke:
2x^2-5x+3>0
Hvala
Treba mi ne resenje vec uputstvo kako da tim sistemom resim ovakve zadatke:
2x^2-5x+3>0
Hvala
pa ima dva resenja:
x1=(-b+sqrt(b^2-4ac))/2a
x2=(-b-sqrt(b^2-4ac))/2a
i to je to.
ako pod korenom dobijes negativnu vrednost (b^2-4ac)<0, onda su resenja kompleksna
ako je pod korenom 0 ima samo jedno resenje
ili ako je pozitivna vrednost imas 2 realna resenja
x1=(-b+sqrt(b^2-4ac))/2a
x2=(-b-sqrt(b^2-4ac))/2a
i to je to.
ako pod korenom dobijes negativnu vrednost (b^2-4ac)<0, onda su resenja kompleksna
ako je pod korenom 0 ima samo jedno resenje
ili ako je pozitivna vrednost imas 2 realna resenja
Rekoh, ne trebaju mi resenja, nego objasnjenje postupka... kako si dosao do vrednosti x1, x2?
Imam standardni oblik kvadratnih (ne)jednacina: ax^2 bx + c.
Treba mi ne resenje vec uputstvo kako da tim sistemom resim ovakve zadatke:
2x^2-5x+3>0
Hvala
Kao sto je Paganko napisao, uzmes kao da je u pitanju jednacina, a ne nejednacina, dakle:
2x[SUP]2[/SUP]-5x+3=0
nadjes reshenja po formuli, nema postupka, jednostavno uvrstis u formulu:
x[SUB]1[/SUB]=(-b+sqrt(b[SUP]2[/SUP]-4ac))/2a
x[SUB]2[/SUB]=(-b-sqrt(b[SUP]2[/SUP]-4ac))/2a
kod tebe je to: x[SUB]1[/SUB]=3/2 i x[SUB]2[/SUB]=1
onda nacrtash brojevnu pravu i obelezis da njoj dve tacke (prvo manju, pa vecu, logicno): 1 i 3/2.
Posto je a(koeficijent uz kvadrtatni chlan)>0, crtas liniju oblika slova U tako da prolazi kroz te dve tachke. Posto ti se trazi da cela nejednachina bude veca od nule, gledash na tom grafiku gde ti je ta funkcija pozitivna,a to je: (-beskonacno, 1) unija (3/2, +beskonacno).
Ovako nekako, samo sa tvojim brojevima:
http://www.thealy.com/LCHM/notes/algebra_files/image025.gif
Ispravite me ako greshim
Poslednja izmena:
уосталом, могла си сама извести ако те занима:
ко вас занима како се дошло до обрасца квадратне једначине, можете видети у следећем примеру: Дата је квадратна једначина са реалним коефицијентима :
Сада ћемо поделити целу једначину са првим коефицијентом (односно поделићемо је са :
У следећем кораку је потребно направити квадрат бинома:
Сада пребацимо познате на десну страну:
Среди се десна страна:
Сада је потребно изразити
Односно, то је:
И када пребацимо
И на крају када се среди, добија се познати образац за израчунавање корена квадратне једначине:
Бакшали рукопис из Индије, датиран у 7. век је садржавао алгебарску формулу за решавање квадратних једначина. Мухамед Ал Хорезми (Персија, 9. век) је развио скуп формула које су радиле за позитивна решења. Абрахам бар Хија (познат и под латинским именом Савасорда) је у Европи увео комплетно решење у својој књизи Liber embadorum из 12. века. Баскара II (1114. – 1185.), индијски математичар и астроном, је дао прво опште решење квадратне једначине са два корена.[3]
Списи кинеског математичара Јанг Хуија (1238. - 1298.) су први у којима се појављују квадратне једначине са негативним коефицијентима од 'x', мада он ово приписује Лиу Јиу.
Poslednja izmena:
Ima li ko kako tacno ide Hewitt Marczewski Pondiczery Theorem za separabilne prostore? Navodno kao posledica te teoreme treba da ispadne da je $R^N$ (prostor svih nizova) separabilan. . . Ako ko zna mozda i gde ima link da se skine lepo kako ide, a ne ovo sa wikipedije i sl. Nego ono bas rad i sl.
Fala!
Fala!
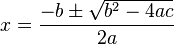
Caka je znaci u formuli, ukapirala.
Dobro, znaci sad zamenjujem varijable u formulu, ali mi nikako ne ispadne 1 i 3/2.
Pazi za x1.
a=1; b=5; c=6
x1= -b+sqrt (b^2-4ac)/2
x1= -5+sqrt(5^2-4 1 6)/2
x1= -5+sqrt (25-24)/2
x1= -5+sqrt1/2
Jesam li negde pogresila, i da li ovaj oblik moze jos da se uprosti?
Dobro, znaci sad zamenjujem varijable u formulu, ali mi nikako ne ispadne 1 i 3/2.
Pazi za x1.
a=1; b=5; c=6
x1= -b+sqrt (b^2-4ac)/2
x1= -5+sqrt(5^2-4 1 6)/2
x1= -5+sqrt (25-24)/2
x1= -5+sqrt1/2
Jesam li negde pogresila, i da li ovaj oblik moze jos da se uprosti?
Baraba na kvadrat
Elita
- Poruka
- 17.135
Da jesi, ceo izraz gore se deli sa dva, probaj tako 
x1= (-b+sqrt (b^2-4ac))/2
x1= (-5+sqrt(5^2-4 1 6))/2
x1= (-5+sqrt (25-24))/2
x1= (-5+sqrt1)/2
kapis?
Nasao sam taj link, ali trazio sam malo opsirnije sta tu jos ima. Jos malo price i po koja lemica da sve upotpuni jer mi je pomalo cudan rezultat pa zato. . .
Hvala u svakom slucaju
aa znam
pa zasto mi onda rezultat nije 3 (kao kod Nebojse), nego -3? x1=(-5+1)/2
x1= -6/2
x= -3
aa znam
x1=(-5+1)/2
x1= -6/2
x= -3
PA ZATO STO JE NEBOJSA LUPIO!!! HAHAHAA
salim se, pa obrati paznju!!!!!!!
a=2
b= - 5
c=3
ti si stavila nejednacinu 2x[SUP]2[/SUP]-5x+3>0, zar ne?
P.S. meni su rezultati 1 i 3/2 (tri polovine), a nema nigde trojke.
Ups
Ajde mi onda objasni zasto si dosao do x1=1, a ja do x1=-3. Gde sam pogresila?
Ajde mi onda objasni zasto si dosao do x1=1, a ja do x1=-3. Gde sam pogresila?
aa znam
x1=(-5+1)/2
x1= -6/2
x= -3
jer si se zaljubila.
(-5+1)/2=-4/2 = -2
to prvo, a drugo:
resim jedan primer pa knjigu u sake i na ucenje!
x[SUP]2[/SUP]-5x+4>0
nule su:
a=1 b=-5 c= 4
x1,x2=(-b+-sqrt(a[SUP]2[/SUP]-4a*c)/2a
x1,x2=(5+-sqrt(25-16))/2
x1,x2=(5+-sqrt(9))/2
x1=(5-3)/2=1
x2=(5+3)/2=4
o.k.
sada zapamti vaznu stvar.
1.sve kvadratne jednacine predstavljaju razne vrste parabola.
2.parabole su okrenute nagore ili nadole u zavisnosti od znaka a. ako je a negatvno onda parabola "gleda na dole", ili matematicki ona je konkavna (ispupcena). Ako je a pozitivno parabola je konveksna odnosno udubljena.
3.parabole imaju preseke sa x osom tamo gde su nule funkcije. Ako dobijes dve nule onda parabola sece x osu na dva mesta. Ako imas jednu nulu onda je dodiruje. Ako imas nijednu nulu onda je cela parabola iznad ili ispod x ose.
x[SUP]2[/SUP]-5x+4=0
ova parabola koja odgovara tvojoj nejednacini ima a=1 pa je konveksna (udubljena) i sece x osu na dva mesta, u tackama x=1 i x=4
sada mozes prosto skicirati takvu krivu u xy ravni:
Pogledajte prilog 68005
sad pogledaj sliku:
za x < 1 i za x>4 imas pozitivna resenja, dok za 1<x<4 imas neativna resenja, pa je jednostavno zakljuciti da resenje tvoje nejednacine ide levo od 1 i desno od 4.
Aj sad 5 zadataka da provezbas, i da skiciras resenje!!!!!!!!
Poslednja izmena:
E, Paganko je objasnio!!!
Vidis da ne zna koliko je -5+1, a ne sta je parabola, konveksnot, konkavnost i slicno... xD
@zmajica92: prvo si dala jedan zadatak, resavas drugi, a pricas o trecem?!
Odluci sta hoces...)
Vidis da ne zna koliko je -5+1, a ne sta je parabola, konveksnot, konkavnost i slicno... xD
@zmajica92: prvo si dala jedan zadatak, resavas drugi, a pricas o trecem?!
Odluci sta hoces...
)- stanje
